Silicon Carbide and Gallium Nitride Crystal Structures

A periodic distribution of groups of atoms (or ions/molecules) is used to create the crystal structure. In an ideal world, when considering a crystal that extends to infinity in spatial coordinates, periodicity translates into translation invariance (or translation symmetry).
The entire crystal is thus formed by the periodic repetition of a fundamental unit known as the unit cell, which can contain groups of atoms/ions/molecules/electrons and is electrically neutral.
The translation symmetry implies that a generic point belonging to an elementary cell has a one-to-one correspondence with a point of the elementary cell obtained by an appropriate translation from the first.
The entire structure can be generated mathematically by three linearly independent vectors (a1, a2, a3) (therefore, not coplanar). To be more specific, the nodes of the lattice are positioned (with respect to a given Cartesian reference Oxyz) by:
Definition 1: Vectors of fundamental translations are a1, a2, and a3, whereas vectors of type n are lattice vectors. The Bravais lattice, also known as the space lattice, is the geometric place.
Definition 2: A parallelepiped, also known as a primitive cell, is identified by the vectors of the fundamental translations.
Assigning a lattice does not imply determining the fundamental translations’ vectors in a unique way. Consider a 2D lattice, as shown in Figure 1, which shows that these vectors can be chosen in a variety of ways.
There can be rotational symmetry with respect to certain axes in addition to translational symmetry. A generic vector n of the lattice is transformed into a vector n′ designated by the same node.
The corresponding symmetries are denoted for the rotations, for example, with C6, C9 for rotations of 60 and 90 and their integer multiples. Then there’s the inversion n n′ = n, followed by the mirror reflection with respect to a given plane. The set of such transformations assumes the algebraic group structure known as the symmetry group of the Bravais lattice by adding the identical transformation n n′ = n.
There are 14 symmetry groups, and thus 14 Bravais lattices, which result in 230 crystal structures.1,2
Wigner-Seitz Cell
As previously stated, the primitive cell can be selected in a variety of ways. In general, it results from a non-conservation of lattice symmetry at the single-cell level.
Figure 2 shows an example of a 2D lattice with obvious hexagonal symmetry. With the primitive cell of choice, we see that this symmetry is not locally conserved, in the sense that the unit cell lacks this symmetry.
Fig. 1: A two-dimensional lattice. The fundamental translation vectors can be chosen in a variety of ways. As a result, the primitive cells are not unique.
Fig. 2:The primitive cell identified by the fundamental translation vectors a1, a2 lacks lattice symmetry..
There is, however, a method for building a primitive cell with the same symmetry as the lattice:
- The segments connecting an assigned node to its neighbors are drawn from that node.
- The perpendicular from each segment is drawn to the midpoint.
The obtained primitive cell has hexagonal symmetry, as illustrated in Figure 3.
Fig. 3: The primitive cell identified using the preceding procedure has the same symmetry as the lattice.
The aforementioned procedure is general in nature, and as such, it reproduces reticular symmetry at the local level, i.e., of a single primitive cell known as a Wigner-Seitz cell.
Hexagonal Lattice And Cubic Lattice
The cubic lattice and the hexagonal lattice are of particular interest in this work. The first is represented as a simple cubic lattice (sc), a body-centered lattice (bcc), and a face-centered lattice (fcc), respectively (Figure 4).
Figure 4 depicts cubic lattice configurations (Source: Introduction to Solid State Physics2). The hexagonal lattice is a three-dimensional extension of the previous lattice. Figure 5 shows how this works.
Fig.5: Hexagonal pattern (Source: Introduction to Solid State Physics2).
Silicon Carbide And Gallium Nitride
We’ve looked at the simpler configurations of Bravais lattices in previous issues; now it’s time to add the “bricks,” or constituent matter (atoms/ions/molecules).
In general, there are molecule or crystal composite systems made up of fundamental units such as atoms. Consider a sodium atom (Na) and a chlorine atom as an example (Cl). The first has an atomic number of Z = 11 and the second has an atomic number of Z = 17. When we “approach” the two atoms, the sodium loses an electron, resulting in the positive ion Na+, and the chlorine gains the lost electron, resulting in the negative ion Cl–.
Electrostatic forces bind these ions together (ionic bond). A molecule is formed as a result of this process. This type of bond is not saturated in the sense that it can propagate (electrostatically) to other ions, resulting in the formation of a specific condensed structure known as an ionic crystal.
Cohesion, on the other hand, occurs in a molecular crystal due to van der Waals forces exerted between molecules such as H2, O2, CO, and various carbon compounds.
Bonds are formed between contiguous atoms thanks to valence electrons. This is true for silicon and germanium:
Si (Z = 14); Ge (Z = 32)
Both have four valence electrons that form bonds with neighboring ones, as illustrated in Figure 6, with each pair of electrons in a spin-singlet state (i.e., antiparallel spin).
Fig. 6: The covalent bond is represented by the colored rectangles.
Silicon carbide and gallium nitride both exhibit a similar configuration, namely a 3D mapping of covalent bonds. The first is rare in nature in the form of a mineral (moissanite), so it is synthesized industrially by starting with carbon and silicon in equal proportions to obtain the same concentration of atoms of both chemical elements.
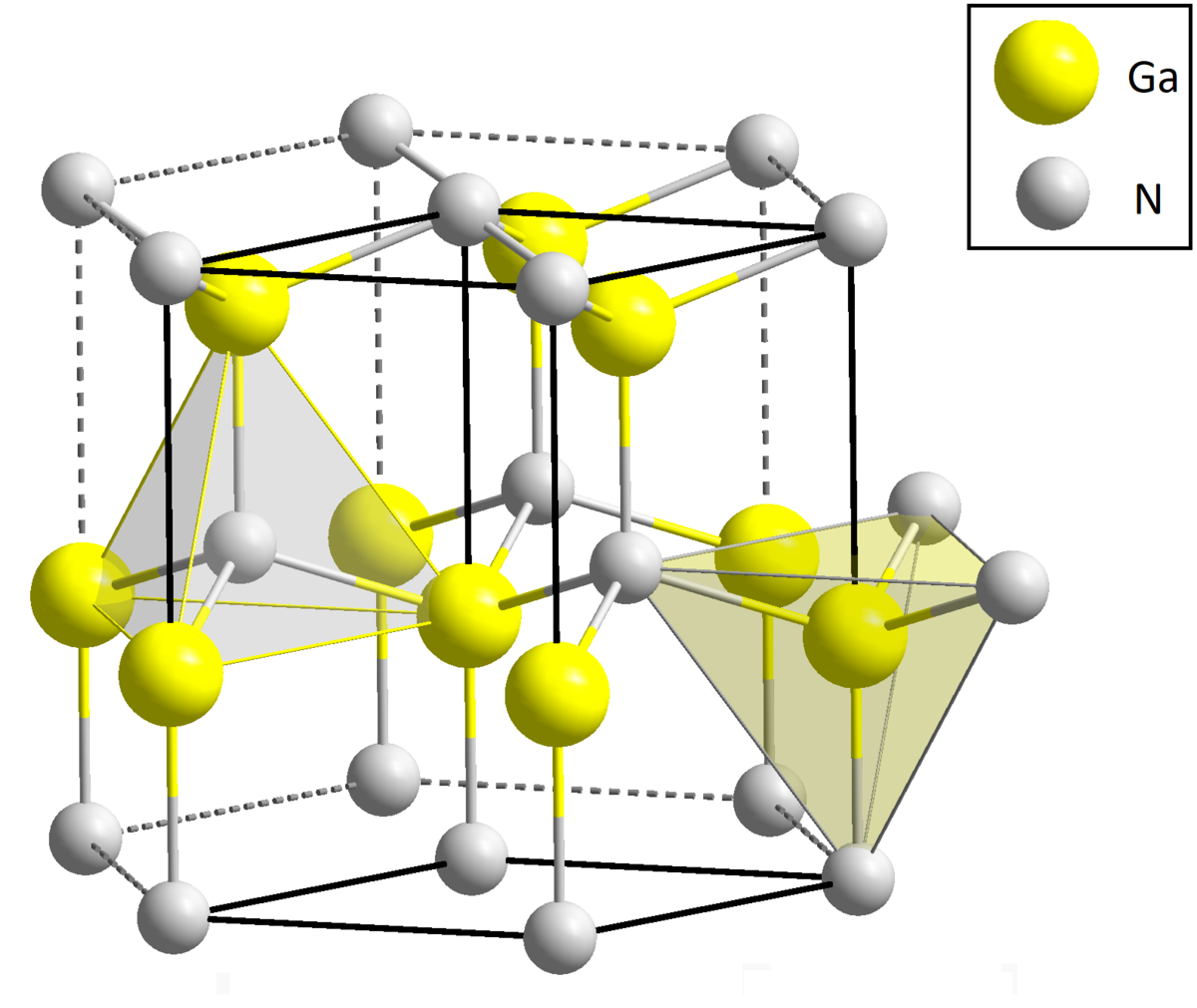
Alpha (-SiC) and beta (-SiC) silicon carbide crystalline forms are of particular interest in technological applications. Alpha’s structure is hexagonal, whereas beta’s structure is face-centered cubic. The symbols H-SiC and C-SiC are frequently used in literature to distinguish the alpha and beta states, i.e., hexagonal and cubic symmetry, respectively.
Silicon carbide has intriguing thermal properties, including a low coefficient of thermal expansion and a high sublimation temperature. As we will see in the following issues, these properties translate into remarkable fallout reliability in power electronics. Whereas gallium nitride occurs naturally in the form of wurtzite (a zinc and iron sulphide), but given the scarcity of diffusion, we attempt to synthesize it.
Given its higher electronic mobility compared to SiC, it performs best in radio-frequency electronics (a physical quantity that we will examine in the next issues). As previously stated, silicon carbide is better suited for power electronics due to its thermal properties, which include high thermal conductivity, which allows for better heat dissipation in the environment.






